Introduction to Sensors + Signal Processing

This reading serves as a breif introduction to sensors. This won’t be a typical reading because there’s a number of good resources already avaliable on the internet for various concepts we will point you to.

What is a Sensor?

Good question! A sensor is also known as a transducer, it essentially reads something from the physical environment and translates it into a signal that a microcontroller or computer can read. We can then use the data from this sensor to do things.

Examples of Sensors

There’s a new and exciting addition to you lab kit this week, it’s a sensor kit! Let’s go ahead and take a look at what’s inside.

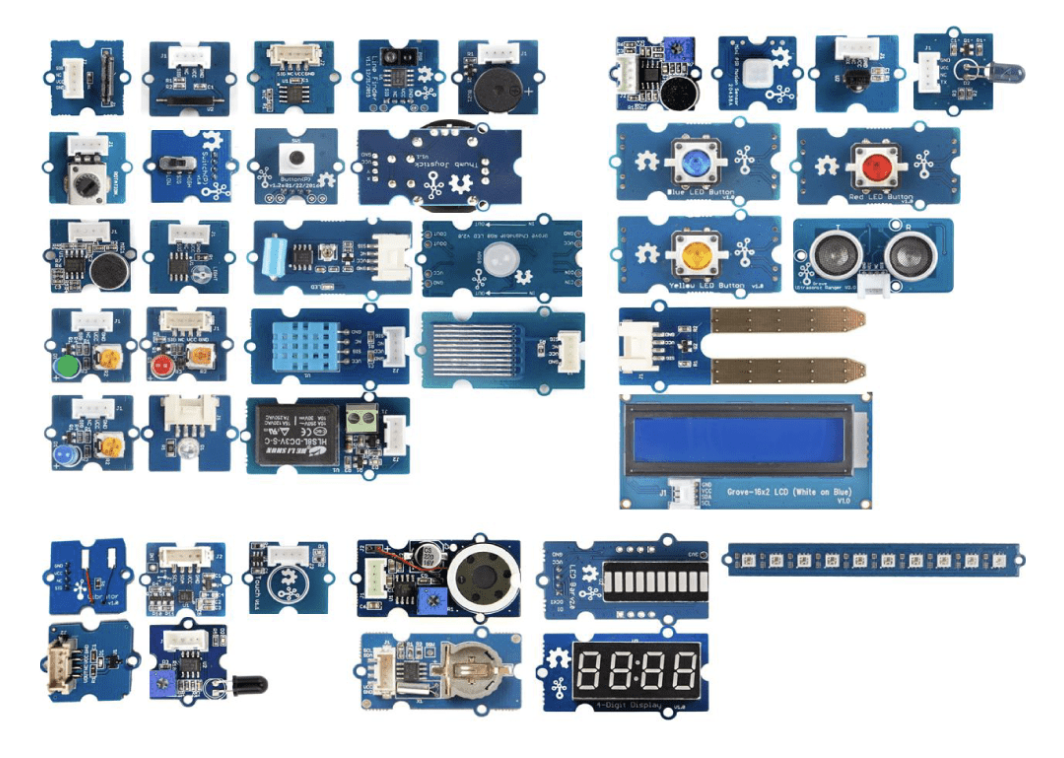
Here’s a non-comprehensive list of sensors the kit includes:

• IR Emitter / Reciever
• Tilt Switch
• Rotary Angle Sensor
• Magnetic Switch
• Thumb Joystick (potentiometer)
• Switches and Buttons
• Temperature Sensor
• Water Sensor
• Sound Sensor
• Light Sensor
• Vibration Sensor
• Temperature and Humidity Sensor
• Hall Sensor (magnetic field strenght)
• Flame Sensor
• Touch Sensor
• Accelerometer (your phone has one of these!)

Each of these sensors reads something from the environment and translates that into a signal that the Arduino can read. So for example, a button when pressed will send an “on” signal to the arduino, and when un-pressed will send an “off” signal to the arduino. A humidity sensor will send a larger signal the more humidity it reads in the room, or a smaller one the less humidity it reads in the room.

Analog and Digital Signals

But what do these signals look like? Let’s ask our good friend, MIT grad, and ex-Next House resident Sal Khan. Fun fact, his old room is now a wifi closet.

We have both types of sensors in our kit analog and digital. The analog sensors output a signal in the range of 0-5V proportional to the information they’re reading from the environment. The digital sensors will just output 0 or 5V. For the button, 0V means on, 5V means off (we will explain why later). Some other sensors might need to transfer numbers digitally, not just “on’s” and “off’s” or might need to translate multiple numbers at a time. For example, the accelerometer needs to transmit the x-acceleration, y-acceleration, and z-acceleration it’s reading. This uses digital communication called I2C (which we will talk about later).

So you might look at the above video and be like digital must be sooooo much better, why would I ever use analog? Well, remember in engineering that there’s no free lunch, there’s always tradeoffs.

Analog signals may be more susceptible to noise, but a true analog signal itself retains 100% of the information you give it. Think about the number pi (3.14159265358979323846264338327950288419716939937510…), how would we translate that with a digital signal? Well we would need infinite bits, meaning our “time” to transfer the data would be infinite since we need to read a bit at a time over a defined time interval. So we have to truncate it. If we used a double data type, we could store 16 digits of pi (3.141592653589793). However, we could concevibly design an analog circuit to produce the exact voltage of pi, it would be hard, but we could do it. When you truncate, you necessarily lose information.

How an ADC will always ruin your day.

So it turns out, however, since a microcontroller is a digital device, the analog signal gets converter to digital anyway using what’s called an ADC. This means no matter what you’ll get what’s called discretization of your signal. Element 14 has a pretty good video on how these work.

The point is your analog signal will get converted to a digital one on the microcontroller anyways. This does not mean you should always use digital, but it does mean you need to think about exactly how much information you need and how little you can ‘get away with.’

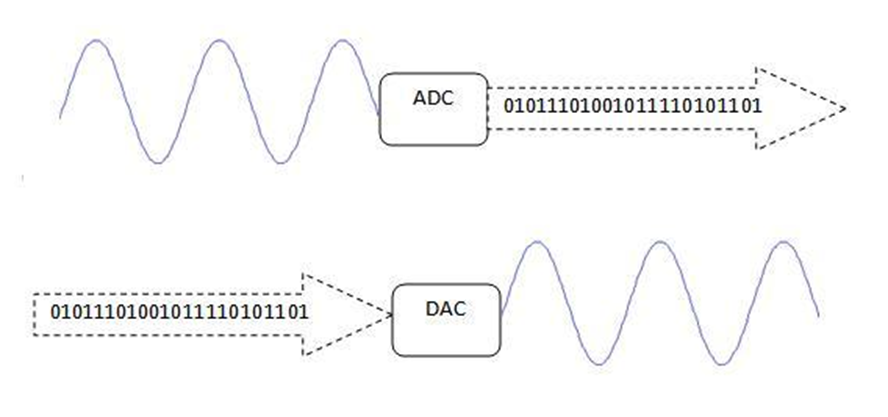
Here’s a good example of how “loss of information” might be detrimental: audio equipment. Ever wonder why cheap bluetooth speakers are so “crackly” or sound “weird?” It has to do with discretization! The information from your phone is being sent as a digital signal to the speaker, the speaker then has to take this and convert it to an analog signal so you can hear (sound is an ANALOG signal, it exists in the real world). This is done through a DAC (Digital-Analog-Converter) which is an ADC but in reverse. Better speakers have better converters (more bits), which retains more information, which makes the sound clearer. The best audio equipment is purely analog (just ask Fender and their guitar amps).

Can I Trust my Sensor?

No. Simply no. Well, it depends on how expensive it is, but then still, no. A sensor will not always give you the correct or true value of the information you’re trying to read. We call this true value the ground truth.

Statistical Model of a Sensor

Generally, a sensor will read values around the ground truth data according to a normal distribution. A normal distribtuion is shown below. Basically, there’s a high probability that you get something close to the true value, and the probability decreases as you get farther away from the true value. A normal distribtion is defined by its mean and standard deviation. The distance between the mean of a sensors distribution and the true value is called the accuracy. The standard deviation is called the precision. If you need a reminder on accuracy vs precision, see the previous reading!

Specifying Accuracy of a Sensor from Allowed Error

Now remember back to the previous reading, we talked about a donkey cart and having an allowed error in our readings. How do we pick a sensor based on an allowed error. Note that the error we specified is the error between two adjacent measurements taken by the sensor.

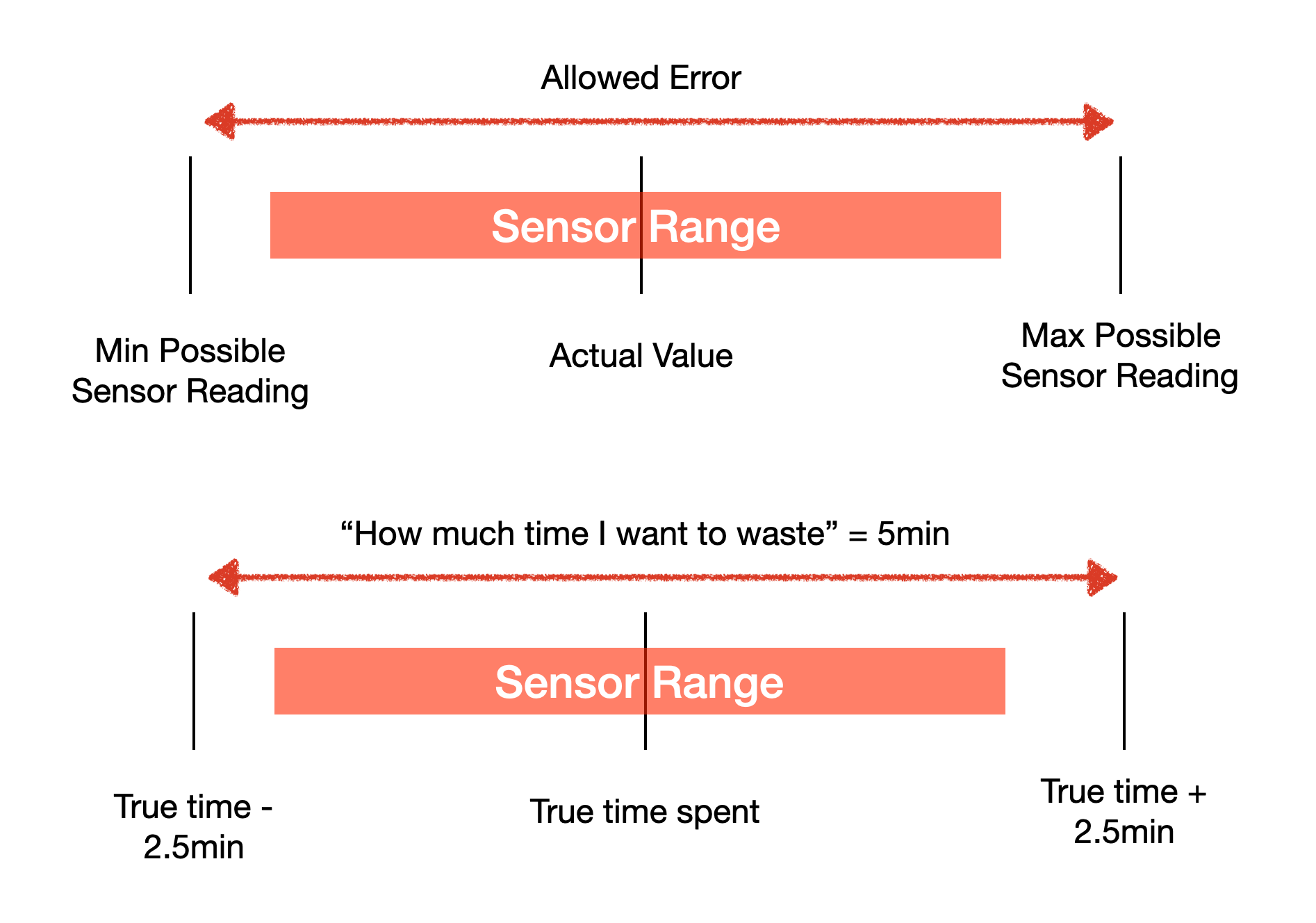
Let’s say I have a sensor with an accuracy of $a,$ then the reading from the sensor could be:

$$T - a <= T <= T + a$$

Where $T$ is the true value the sensor is trying to measure. But we’re continuously measuring the sensor right? Every so often we’re going to take a new measurement. And the maximum “error” between any two measurements can be given based on the following.

$$T_1 - a <= T_1 <= T_1 + a$$ $$T_2 - a <= T_2 <= T_2 + a$$

The maximum error is when the sensor reads the highest value it possibly can, and it reads the lowest value it possibly can. And vice versa.

$$(T_2 - a) - (T_1 + a) <= T_2-T_1 <= (T_2 - a) - (T_1 + a)$$ $$(T_2 - T_1) - 2a <= T_2-T_1 <= (T_2 - T_2) + 2a$$

If you didn’t follow this math, that’s OK. But the main idea, is you need your sensors to have an accuracy twice as good as your allowable error range. Note that this calculation assumes that the error above and below the true value are symmetric, it’s possible for this to be asymmetric. But for now, we won’t cover that.

But now how do I determine what the accuract of my sensor is? Well the datasheet will tell you! Let’s take a look at a sensor.

The sensor we linked is a Grove CO2 sensor with a quoted accuracy of ±(30 ppm + 3%). That means it will measure the number of particles of CO2 in the air between 400ppm to 10000ppm within ±(30 ppm). Which means if we cared about the change in CO2 concentration from measurement to measurement, we could get an accuracy of around 60ppm.

Things to include in the future

• basic filtration
• shifted process distribution
• better explination of everything